Reinforcement Learning Tutorial

Our Reinforcement learning tutorial will give you a complete overview of reinforcement learning, including MDP and Q-learning. In RL tutorial, you will learn the below topics:

• What is Reinforcement Learning?
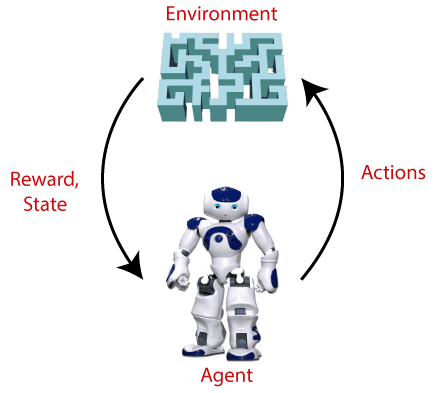
• Terms used in Reinforcement Learning.
• Key features of Reinforcement Learning.
• Elements of Reinforcement Learning.
• Approaches to implementing Reinforcement Learning.
• How does Reinforcement Learning Work?
• The Bellman Equation.
• Types of Reinforcement Learning.
• Reinforcement Learning Algorithm.
• Markov Decision Process.
• What is Q-Learning?
• Difference between Supervised Learning and Reinforcement Learning.
• Applications of Reinforcement Learning.
• Conclusion.

What is Reinforcement Learning?

• Reinforcement Learning is a feedback-based Machine learning technique in which an agent learns to behave in an environment by performing the actions and seeing the results of actions. For each good action, the agent gets positive feedback, and for each bad action, the agent gets negative feedback or penalty.
• In Reinforcement Learning, the agent learns automatically using feedbacks without any labeled data, unlike supervised learning.
• Since there is no labeled data, so the agent is bound to learn by its experience only.
• RL solves a specific type of problem where decision making is sequential, and the goal is long-term, such as game-playing, robotics, etc.
• The agent interacts with the environment and explores it by itself. The primary goal of an agent in reinforcement learning is to improve the performance by getting the maximum positive rewards.
• The agent learns with the process of hit and trial, and based on the experience, it learns to perform the task in a better way. Hence, we can say that "Reinforcement learning is a type of machine learning method where an intelligent agent (computer program) interacts with the environment and learns to act within that." How a Robotic dog learns the movement of his arms is an example of Reinforcement learning.
• It is a core part of Artificial intelligence, and all AI agent works on the concept of reinforcement learning. Here we do not need to pre-program the agent, as it learns from its own experience without any human intervention.
• Example: Suppose there is an AI agent present within a maze environment, and his goal is to find the diamond. The agent interacts with the environment by performing some actions, and based on those actions, the state of the agent gets changed, and it also receives a reward or penalty as feedback.
• The agent continues doing these three things (take action, change state/remain in the same state, and get feedback), and by doing these actions, he learns and explores the environment.
• The agent learns that what actions lead to positive feedback or rewards and what actions lead to negative feedback penalty. As a positive reward, the agent gets a positive point, and as a penalty, it gets a negative point.

Terms used in Reinforcement Learning

• Agent(): An entity that can perceive/explore the environment and act upon it.
• Environment(): A situation in which an agent is present or surrounded by. In RL, we assume the stochastic environment, which means it is random in nature.
• Action(): Actions are the moves taken by an agent within the environment.
• State(): State is a situation returned by the environment after each action taken by the agent.
• Reward(): A feedback returned to the agent from the environment to evaluate the action of the agent.
• Policy(): Policy is a strategy applied by the agent for the next action based on the current state.
• Value(): It is expected long-term retuned with the discount factor and opposite to the short-term reward.
• Q-value(): It is mostly similar to the value, but it takes one additional parameter as a current action (a).

Key Features of Reinforcement Learning

• In RL, the agent is not instructed about the environment and what actions need to be taken.
• It is based on the hit and trial process.
• The agent takes the next action and changes states according to the feedback of the previous action.
• The agent may get a delayed reward.
• The environment is stochastic, and the agent needs to explore it to reach to get the maximum positive rewards.

Approaches to implement Reinforcement Learning

There are mainly three ways to implement reinforcement-learning in ML, which are:

1. Value-based:
   The value-based approach is about to find the optimal value function, which is the maximum value at a state under any policy. Therefore, the agent expects the long-term return at any state(s) under policy π.
2. Policy-based:
   Policy-based approach is to find the optimal policy for the maximum future rewards without using the value function. In this approach, the agent tries to apply such a policy that the action performed in each step helps to maximize the future reward.
   The policy-based approach has mainly two types of policy:
   • Deterministic: The same action is produced by the policy (π) at any state.
   • Stochastic: In this policy, probability determines the produced action.
3. Model-based: In the model-based approach, a virtual model is created for the environment, and the agent explores that environment to learn it. There is no particular solution or algorithm for this approach because the model representation is different for each environment.

Elements of Reinforcement Learning

There are four main elements of Reinforcement Learning, which are given below:

1. Policy
2. Reward Signal
3. Value Function
4. Model of the environment

1) Policy: A policy can be defined as a way how an agent behaves at a given time. It maps the perceived states of the environment to the actions taken on those states. A policy is the core element of the RL as it alone can define the behavior of the agent. In some cases, it may be a simple function or a lookup table, whereas, for other cases, it may involve general computation as a search process. It could be deterministic or a stochastic policy:

For deterministic policy: a = π(s)
For stochastic policy: π(a | s) = P[At =a | St = s]

2) Reward Signal: The goal of reinforcement learning is defined by the reward signal. At each state, the environment sends an immediate signal to the learning agent, and this signal is known as a reward signal. These rewards are given according to the good and bad actions taken by the agent. The agent's main objective is to maximize the total number of rewards for good actions. The reward signal can change the policy, such as if an action selected by the agent leads to low reward, then the policy may change to select other actions in the future.

3) Value Function: The value function gives information about how good the situation and action are and how much reward an agent can expect. A reward indicates the immediate signal for each good and bad action, whereas a value function specifies the good state and action for the future. The value function depends on the reward as, without reward, there could be no value. The goal of estimating values is to achieve more rewards.

4) Model: The last element of reinforcement learning is the model, which mimics the behavior of the environment. With the help of the model, one can make inferences about how the environment will behave. Such as, if a state and an action are given, then a model can predict the next state and reward.

The model is used for planning, which means it provides a way to take a course of action by considering all future situations before actually experiencing those situations. The approaches for solving the RL problems with the help of the model are termed as the model-based approach. Comparatively, an approach without using a model is called a model-free approach.

How does Reinforcement Learning Work?

To understand the working process of the RL, we need to consider two main things:

• Environment: It can be anything such as a room, maze, football ground, etc.
• Agent: An intelligent agent such as AI robot.

Let's take an example of a maze environment that the agent needs to explore. Consider the below image: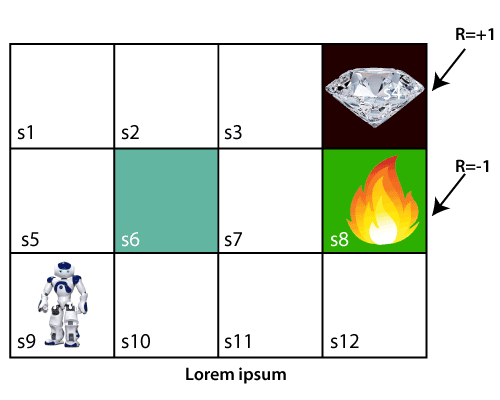

In the above image, the agent is at the very first block of the maze. The maze is consisting of an S₆ block, which is a wall, S₈ a fire pit, and S₄ a diamond block.

The agent cannot cross the S₆ block, as it is a solid wall. If the agent reaches the S₄ block, then get the +1 reward; if it reaches the fire pit, then gets -1 reward point. It can take four actions: move up, move down, move left, and move right.

The agent can take any path to reach to the final point, but he needs to make it in possible fewer steps. Suppose the agent considers the path S9-S5-S1-S2-S3, so he will get the +1-reward point.

The agent will try to remember the preceding steps that it has taken to reach the final step. To memorize the steps, it assigns 1 value to each previous step. Consider the below step: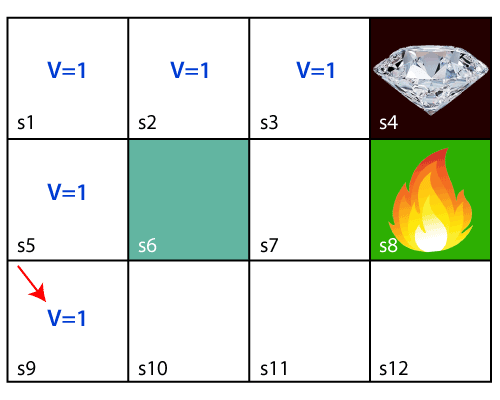

Now, the agent has successfully stored the previous steps assigning the 1 value to each previous block. But what will the agent do if he starts moving from the block, which has 1 value block on both sides? Consider the below diagram: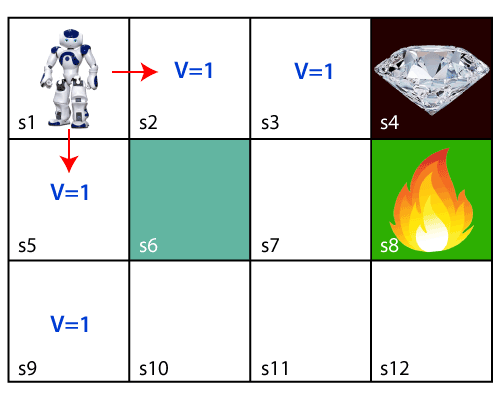

It will be a difficult condition for the agent whether he should go up or down as each block has the same value. So, the above approach is not suitable for the agent to reach the destination. Hence to solve the problem, we will use the Bellman equation, which is the main concept behind reinforcement learning.

The Bellman Equation

The Bellman equation was introduced by the Mathematician Richard Ernest Bellman in the year 1953, and hence it is called as a Bellman equation. It is associated with dynamic programming and used to calculate the values of a decision problem at a certain point by including the values of previous states.

It is a way of calculating the value functions in dynamic programming or environment that leads to modern reinforcement learning.

The key-elements used in Bellman equations are:

• Action performed by the agent is referred to as "a"
• State occurred by performing the action is "s."
• The reward/feedback obtained for each good and bad action is "R."
• A discount factor is Gamma "γ."

The Bellman equation can be written as:

Where,

V(s)= value calculated at a particular point.

R(s,a) = Reward at a particular state s by performing an action.

γ = Discount factor

V(s`) = The value at the previous state.

In the above equation, we are taking the max of the complete values because the agent tries to find the optimal solution always.

So now, using the Bellman equation, we will find value at each state of the given environment. We will start from the block, which is next to the target block.

For 1st block:

V(s3) = max [R(s,a) + γV(s`)], here V(s')= 0 because there is no further state to move.

V(s3)= max[R(s,a)]=> V(s3)= max[1]=> V(s3)= 1.

For 2nd block:

V(s2) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 1, and R(s, a)= 0, because there is no reward at this state.

V(s2)= max[0.9(1)]=> V(s)= max[0.9]=> V(s2) =0.9

For 3rd block:

V(s1) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 0.9, and R(s, a)= 0, because there is no reward at this state also.

V(s1)= max[0.9(0.9)]=> V(s3)= max[0.81]=> V(s1) =0.81

For 4th block:

V(s5) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 0.81, and R(s, a)= 0, because there is no reward at this state also.

V(s5)= max[0.9(0.81)]=> V(s5)= max[0.81]=> V(s5) =0.73

For 5th block:

V(s9) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 0.73, and R(s, a)= 0, because there is no reward at this state also.

V(s9)= max[0.9(0.73)]=> V(s4)= max[0.81]=> V(s4) =0.66

Consider the below image: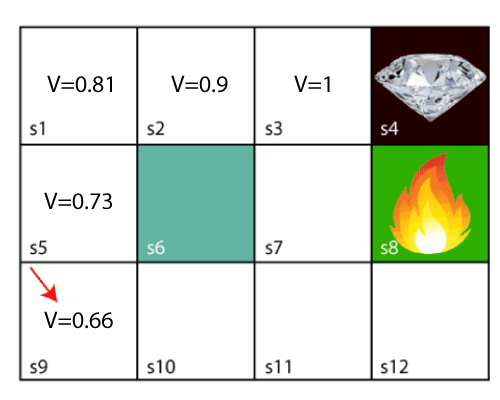

Now, we will move further to the 6^th block, and here agent may change the route because it always tries to find the optimal path. So now, let's consider from the block next to the fire pit.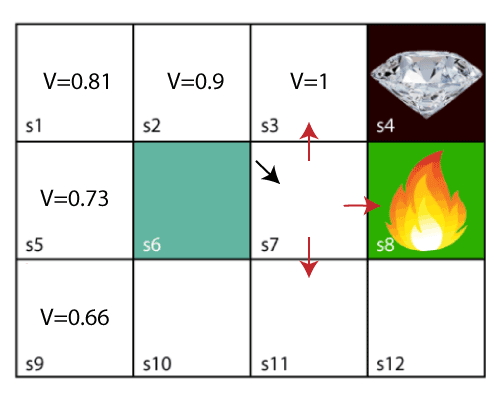

Now, the agent has three options to move; if he moves to the blue box, then he will feel a bump if he moves to the fire pit, then he will get the -1 reward. But here we are taking only positive rewards, so for this, he will move to upwards only. The complete block values will be calculated using this formula. Consider the below image:

Types of Reinforcement learning

There are mainly two types of reinforcement learning, which are:

• Positive Reinforcement
• Negative Reinforcement

Positive Reinforcement:

The positive reinforcement learning means adding something to increase the tendency that expected behavior would occur again. It impacts positively on the behavior of the agent and increases the strength of the behavior.

This type of reinforcement can sustain the changes for a long time, but too much positive reinforcement may lead to an overload of states that can reduce the consequences.

Negative Reinforcement:

The negative reinforcement learning is opposite to the positive reinforcement as it increases the tendency that the specific behavior will occur again by avoiding the negative condition.

It can be more effective than the positive reinforcement depending on situation and behavior, but it provides reinforcement only to meet minimum behavior.

How to represent the agent state?

We can represent the agent state using the Markov State that contains all the required information from the history. The State St is Markov state if it follows the given condition:

P[St+1 | St ] = P[St +1 | S1,......, St]
    

Markov Decision Process

Markov Decision Process or MDP, is used to formalize the reinforcement learning problems. If the environment is completely observable, then its dynamic can be modeled as a Markov Process. In MDP, the agent constantly interacts with the environment and performs actions; at each action, the environment responds and generates a new state.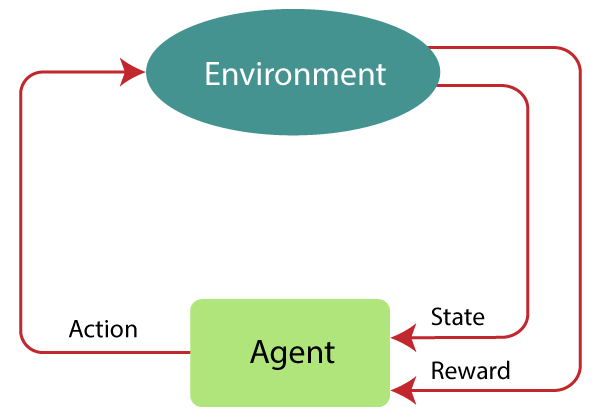

MDP is used to describe the environment for the RL, and almost all the RL problem can be formalized using MDP.

MDP contains a tuple of four elements (S, A, P_a, R_a):

• A set of finite States S
• A set of finite Actions A
• Rewards received after transitioning from state S to state S', due to action a.
• Probability P_a.

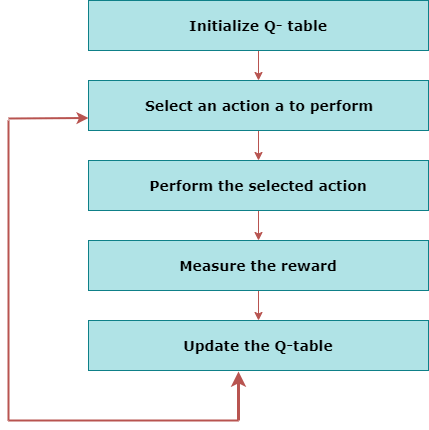
MDP uses Markov property, and to better understand the MDP, we need to learn about it.

Markov Property:

It says that "If the agent is present in the current state S1, performs an action a1 and move to the state s2, then the state transition from s1 to s2 only depends on the current state and future action and states do not depend on past actions, rewards, or states."

Or, in other words, as per Markov Property, the current state transition does not depend on any past action or state. Hence, MDP is an RL problem that satisfies the Markov property. Such as in a Chess game, the players only focus on the current state and do not need to remember past actions or states.

Finite MDP:

A finite MDP is when there are finite states, finite rewards, and finite actions. In RL, we consider only the finite MDP.

Markov Process:

Markov Process is a memoryless process with a sequence of random states S₁, S₂, ....., S_t that uses the Markov Property. Markov process is also known as Markov chain, which is a tuple (S, P) on state S and transition function P. These two components (S and P) can define the dynamics of the system.

Reinforcement Learning Algorithms

Reinforcement learning algorithms are mainly used in AI applications and gaming applications. The main used algorithms are:

• Q-Learning:
  • Q-learning is an Off policy RL algorithm, which is used for the temporal difference Learning. The temporal difference learning methods are the way of comparing temporally successive predictions.
  • It learns the value function Q (S, a), which means how good to take action "a" at a particular state "s."
  • The below flowchart explains the working of Q- learning: